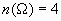Unidad 3

Aplicacion de la Distribución de Probabilidad

En el Laboratorio de Control y Automatización de la FIEE de la UNAC se tiene 16 computadoras, el Jefe de dicho laboratorio reporta el siguiente informe:

Distribución de Probabilidad de Poisson

Describe la cantidad de veces que ocurre un evento en un intervalo determinado (tiempo, volumen, temperatura, etc...).La distribución se basa en dos supuestos:

1°) La probabilidad es proporcional a la extensión del intervalo.

2°) Los intervalos son independientes.

Esta distribución es una forma límite de la distribución binomial,cuando la probabilidad de éxito es bien pequeña y n es grande ,a esta distribución se llama " Ley de eventos improbables", lo cual significa que la probabilidad de p es bien pequeña .

La probabilidad de Poisson es una probabilidad discreta; puesto que se forma por conteo










Donde:








Media del número de ocurrencias








Constante de Euler.





x : Número de ocurrencias






Media:-Esta dado por:

distribucion de probabilid Hipergeometrica

Esta distribución se aplica cuando el muestreo se realiza sin repetición y la probabilidad de éxito no permanece constante de un ensayo a otros calcula mediante la fórmula:

Donde:
N: Tamaño de la población
S: Cantidad de éxitos en la población
X: Número de éxitos en la muestra.
n : Tamaño de la muestra.
n>=0.05N

Distribucion de Probabilidad Acumulada

Estos son similares a las distribuciones acumuladas, así aplicamos para las distribuciones binomiales.

VARIABLE ALEATORIA X

P=0.60 Probabilidades

0

0.004

1

0.0037

2

0.0138

3

0.276.

4

0.311

P(x<=2)=P(x=0)+P(x=1)+P(x=2)

Distribución de la Probabilidad Binomial

Esta distribución es la que mejor se ajusta a la distribución de probabilidades de variable discreta.

Si lanzamos dos monedas al aire, se tiene el siguiente espacio maestral:

Si p es la probabilidad de obtener una cara(c) al considerar una sola moneda y q la probabilidad de que salga sello(s); entonces p=q= ½; luego:

Con el binomio de Newton deducimos lo siguiente:

Luego, la distribución de probabilidad binimial esta dada por:

Donde:
p: Probabilidad de éxito de cada ensayo.
n: Número de ensayos.
x: Número de exitos.

OBSERVACIÓN

Si p=q=1/2, el histograma de las distribuciones binomiales son simétricas.Si el experimento se repite r veces con n ensayos ; entonces se tiene:

Luego se deduce que:

MEDIA DE LA DISTRIBUCIÓN BINOMIAL
Esta dada por:

VARIANZA DE LA DISTRIBUCIÓN BINOMIAL

Varianza

Mide el grado de dispersión de la distribución de probabilidades, siendo la formula:


También se aplica la fórmula:

Desviación Estándar.-Es la raíz cuadrad del varianza, luego: