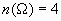miércoles, 13 de enero de 2010
Aplicacion de la Distribución de Probabilidad
En el Laboratorio de Control y Automatización de la FIEE de la UNAC se tiene 16 computadoras, el Jefe de dicho laboratorio reporta el siguiente informe:
Distribución de Probabilidad de Poisson
Describe la cantidad de veces que ocurre un evento en un intervalo determinado (tiempo, volumen, temperatura, etc...).La distribución se basa en dos supuestos:
1°) La probabilidad es proporcional a la extensión del intervalo.
2°) Los intervalos son independientes.
Esta distribución es una forma límite de la distribución binomial,cuando la probabilidad de éxito es bien pequeña y n es grande ,a esta distribución se llama " Ley de eventos improbables", lo cual significa que la probabilidad de p es bien pequeña .
La probabilidad de Poisson es una probabilidad discreta; puesto que se forma por conteo
Donde:
Media del número de ocurrencias
Constante de Euler.
x : Número de ocurrencias
Media:-Esta dado por:
1°) La probabilidad es proporcional a la extensión del intervalo.
2°) Los intervalos son independientes.
Esta distribución es una forma límite de la distribución binomial,cuando la probabilidad de éxito es bien pequeña y n es grande ,a esta distribución se llama " Ley de eventos improbables", lo cual significa que la probabilidad de p es bien pequeña .
La probabilidad de Poisson es una probabilidad discreta; puesto que se forma por conteo
Donde:
Media del número de ocurrencias
Constante de Euler.
x : Número de ocurrencias
Media:-Esta dado por:
distribucion de probabilid Hipergeometrica
Esta distribución se aplica cuando el muestreo se realiza sin repetición y la probabilidad de éxito no permanece constante de un ensayo a otros calcula mediante la fórmula:
Donde:
N: Tamaño de la población
S: Cantidad de éxitos en la población
X: Número de éxitos en la muestra.
n : Tamaño de la muestra.
n>=0.05N
Donde:N: Tamaño de la población
S: Cantidad de éxitos en la población
X: Número de éxitos en la muestra.
n : Tamaño de la muestra.
n>=0.05N
Distribucion de Probabilidad Acumulada
Estos son similares a las distribuciones acumuladas, así aplicamos para las distribuciones binomiales.
VARIABLE ALEATORIA X
VARIABLE ALEATORIA X
P=0.60 Probabilidades
0
0.004
1
0.0037
2
0.0138
3
0.276.
4
0.311
P(x<=2)=P(x=0)+P(x=1)+P(x=2)
martes, 12 de enero de 2010
Distribución de la Probabilidad Binomial
Esta distribución es la que mejor se ajusta a la distribución de probabilidades de variable discreta. 
Si lanzamos dos monedas al aire, se tiene el siguiente espacio maestral:
Si p es la probabilidad de obtener una cara(c) al considerar una sola moneda y q la probabilidad de que salga sello(s); entonces p=q= ½; luego:
Con el binomio de Newton deducimos lo siguiente:
Luego, la distribución de probabilidad binimial esta dada por:
Donde:
p: Probabilidad de éxito de cada ensayo.
n: Número de ensayos.
x: Número de exitos.
OBSERVACIÓN
Si p=q=1/2, el histograma de las distribuciones binomiales son simétricas.Si el experimento se repite r veces con n ensayos ; entonces se tiene:
Luego se deduce que:
MEDIA DE LA DISTRIBUCIÓN BINOMIAL
Esta dada por: 
VARIANZA DE LA DISTRIBUCIÓN BINOMIAL
Varianza
Mide el grado de dispersión de la distribución de probabilidades, siendo la formula:
También se aplica la fórmula:
Desviación Estándar.-Es la raíz cuadrad del varianza, luego:
También se aplica la fórmula:
Desviación Estándar.-Es la raíz cuadrad del varianza, luego:
Variable Aleatoria
Cantidad que es resultado de un experimento y debido al azar, puede tomar valores diferentes.
Variable aleatoria discreta:- Toma valores claramente separados, generalmente se produce por conteo.
Variable aleatoria continua:-Cantidades que toman infinitos valores, dentro de un rango permitido, generándose una distribución de probabilidades continuas.
Media de una Distribución de Probabilidades.-Valor promedio a largo plazo de la variable aleatoria, también es conocido como valor esperado. Esta media es un promedio ponderado, en el que los valores posibles se ponderan mediante sus probabilidades correspondientes de ocurrencia, se calcula con la formula:
Donde P(X) es la probabilidad que puede tomar la variable aleatoria X.
Variable aleatoria discreta:- Toma valores claramente separados, generalmente se produce por conteo.
Variable aleatoria continua:-Cantidades que toman infinitos valores, dentro de un rango permitido, generándose una distribución de probabilidades continuas.
Media de una Distribución de Probabilidades.-Valor promedio a largo plazo de la variable aleatoria, también es conocido como valor esperado. Esta media es un promedio ponderado, en el que los valores posibles se ponderan mediante sus probabilidades correspondientes de ocurrencia, se calcula con la formula:
Donde P(X) es la probabilidad que puede tomar la variable aleatoria X.
Distribucion de Probabilidades
Muestra todos los resultados posibles de un experimento y la probabilidad de cada resultado.
¿Cómo generamos una distribución de probabilidad?
Supongamos que se quiere saber el numero de caras que se obtienen al lanzar cuatro veces una moneda al aire?
Es obvio que, el hecho de que la modena caiga de costado se descarta.
Los posibles resultados son: cero caras, una cara, dos caras, tres caras y cuatro caras.
Si realizamos el experimento obtenemos el siguiente espacio muestral:
NUMERO DE CARAS FRECUENCIA DISTRIBUCIÓN DE PROBABILIDADES
0 1 1/16
1 4 4/16
2 6 6/16
3 4 4/16
4 1 1/16
¿Cómo generamos una distribución de probabilidad?
Supongamos que se quiere saber el numero de caras que se obtienen al lanzar cuatro veces una moneda al aire?
Es obvio que, el hecho de que la modena caiga de costado se descarta.
Los posibles resultados son: cero caras, una cara, dos caras, tres caras y cuatro caras.
Si realizamos el experimento obtenemos el siguiente espacio muestral:
NUMERO DE CARAS FRECUENCIA DISTRIBUCIÓN DE PROBABILIDADES
0 1 1/16
1 4 4/16
2 6 6/16
3 4 4/16
4 1 1/16
Diagrama de Arbol
Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.
En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).
Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.
Ejemplo:
Sea lanza una moneda cargada, a favor del lado del águila, si cae águila la moneda se saca una bola de una urna A en caso contrario de la urna B, la urna A tiene objetos de tipo s, la urna B objetos de tipo r, se sabe que por el contrario la urna B tiene objetos de tipo s y r, pero no la misma cantidad.
Bosqueje mediante un diagrama de árbol la solución, a fin de encontrar la probabilidad.
Probabilidades
La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro.
Con este fin, introduciremos algunas definiciones:
Suceso:
Es cada uno de los resultados posibles de una experiencia aleatoria.
Al lanzar una moneda salga cara.
Al lanzar una moneda se obtenga 4.
Espacio muestral:
Es el conjunto de todos los posibles resultados de una experiencia aleatoria, lo representaremos por E (o bien por la letra griega Ω).
Espacio muestral de una moneda:
E = {C, X}.
Espacio muestral de un dado:
E = {1, 2, 3, 4, 5, 6}.
Suceso aleatorio:
Suceso aleatorio es cualquier subconjunto del espacio muestral.
Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.
Ejemplo
Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:
1. El espacio muestral.
E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}
2. El suceso A = {extraer tres bolas del mismo color}.
B = {(b,b,b); (n, n,n)}
3. El suceso A = {extraer al menos una bola blanca}.
B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}
4. El suceso A = {extraer una sola bola negra}.
A = {(b,b,n); (b,n,b); (n,b,b)}
Con este fin, introduciremos algunas definiciones:
Suceso:
Es cada uno de los resultados posibles de una experiencia aleatoria.
Al lanzar una moneda salga cara.
Al lanzar una moneda se obtenga 4.
Espacio muestral:
Es el conjunto de todos los posibles resultados de una experiencia aleatoria, lo representaremos por E (o bien por la letra griega Ω).
Espacio muestral de una moneda:
E = {C, X}.
Espacio muestral de un dado:
E = {1, 2, 3, 4, 5, 6}.
Suceso aleatorio:
Suceso aleatorio es cualquier subconjunto del espacio muestral.
Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.
Ejemplo
Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:
1. El espacio muestral.
E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}
2. El suceso A = {extraer tres bolas del mismo color}.
B = {(b,b,b); (n, n,n)}
3. El suceso A = {extraer al menos una bola blanca}.
B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}
4. El suceso A = {extraer una sola bola negra}.
A = {(b,b,n); (b,n,b); (n,b,b)}
lunes, 11 de enero de 2010
Varianza
Como forma de medir la dispersión de los datos hemos descartado:
,pues sabemos que esa suma vale 0, ya que las desviaciones con respecto a la media se compensan al haber términos en esa suma que son de signos distintos.
Para tener el mismo signo al sumar las desviaciones con respecto a la media podemos realizar la suma con valores absolutos. Esto nos lleva a la Dm, pero como hemos mencionado, tiene poco interés por las dificultades que presenta.
Si las desviaciones con respecto a la media las consideramos al cuadrado, , de nuevo obtenemos que todos los sumandos tienen el mismo signo (positivo). Esta es además la forma de medir la dispersión de los datos de forma que sus propiedades matemáticas son más fáciles de utilizar.
Vamos a definir entonces dos estadísticos que serán fundamentales en el resto del curso: La varianza y la desviación típica.
La varianza, , se define como la media de las diferencias cuadráticas de n puntuaciones con respecto a su media aritmética, es decir Para datos agrupados en tablas, usando las notaciones establcidas en los capítulos anteriores, la varianza se puede escibir como Una fórmula equivalente para el cálculo de la varianza.
La varianza no tiene la misma magnitud que las observaciones (ej. si las observaciones se miden en metros, la varianza lo hace en ). Si queremos que la medida de dispersión sea de la misma dimensionalidad que las observaciones bastará con tomar su raíz cuadrada.
Ejemplo
Calcular la varianza y desviación típica de las siguientes cantidades medidas en metros:
3,3,4,4,5
Solución: Para calcular dichas medidas de dispersión es necesario calcular previamente el valor con respecto al cual vamos a medir las diferencias.
siendo la desviación típica su raíz cuadrada:
Las siguientes propiedades de la varianza (respectivamente, desviación típica) son importantes a la hora de hacer un cambio de origen y escala a una variable. En primer lugar, la varianza (resp. Desviación típica) no se ve afectada si al conjunto de valores de la variable se le añade una constante. Si además cada observación es multiplicada por otra constante, en este caso la varianza cambia en relación al cuadrado de la constante (resp. La desviación típica cambia en relación al valor absoluto de la constante).
,pues sabemos que esa suma vale 0, ya que las desviaciones con respecto a la media se compensan al haber términos en esa suma que son de signos distintos.
Para tener el mismo signo al sumar las desviaciones con respecto a la media podemos realizar la suma con valores absolutos. Esto nos lleva a la Dm, pero como hemos mencionado, tiene poco interés por las dificultades que presenta.
Si las desviaciones con respecto a la media las consideramos al cuadrado, , de nuevo obtenemos que todos los sumandos tienen el mismo signo (positivo). Esta es además la forma de medir la dispersión de los datos de forma que sus propiedades matemáticas son más fáciles de utilizar.
Vamos a definir entonces dos estadísticos que serán fundamentales en el resto del curso: La varianza y la desviación típica.
La varianza, , se define como la media de las diferencias cuadráticas de n puntuaciones con respecto a su media aritmética, es decir Para datos agrupados en tablas, usando las notaciones establcidas en los capítulos anteriores, la varianza se puede escibir como Una fórmula equivalente para el cálculo de la varianza.
La varianza no tiene la misma magnitud que las observaciones (ej. si las observaciones se miden en metros, la varianza lo hace en ). Si queremos que la medida de dispersión sea de la misma dimensionalidad que las observaciones bastará con tomar su raíz cuadrada.
Ejemplo
Calcular la varianza y desviación típica de las siguientes cantidades medidas en metros:
3,3,4,4,5
Solución: Para calcular dichas medidas de dispersión es necesario calcular previamente el valor con respecto al cual vamos a medir las diferencias.
siendo la desviación típica su raíz cuadrada:
Las siguientes propiedades de la varianza (respectivamente, desviación típica) son importantes a la hora de hacer un cambio de origen y escala a una variable. En primer lugar, la varianza (resp. Desviación típica) no se ve afectada si al conjunto de valores de la variable se le añade una constante. Si además cada observación es multiplicada por otra constante, en este caso la varianza cambia en relación al cuadrado de la constante (resp. La desviación típica cambia en relación al valor absoluto de la constante).
Medidas de Variabilidad
Los estadísticos de tendencia central o posición nos indican donde se sitúa un grupo de puntuaciones. Los de variabilidad o dispersión nos indican si esas puntuaciones o valores están próximas entre sí o si por el contrario están o muy dispersas.
Una medida razonable de la variabilidad podría ser la amplitud o rango, que se obtiene restando el valor más bajo de un conjunto de observaciones del valor más alto. Es fácil de calcular y sus unidades son las mismas que las de la variable, aunque posee varios inconvenientes:
Una medida razonable de la variabilidad podría ser la amplitud o rango, que se obtiene restando el valor más bajo de un conjunto de observaciones del valor más alto. Es fácil de calcular y sus unidades son las mismas que las de la variable, aunque posee varios inconvenientes:
- No utiliza todas las observaciones (sólo dos de ellas);
- Se puede ver muy afectada por alguna observación extrema;
- El rango aumenta con el número de observaciones, o bien se queda igual. En cualquier caso nunca disminuye.
En el transcurso de esta sección, veremos medidas de dispersión mejores que la anterior. Estas se determinan en función de la distancia entre las observaciones y algun estadístico de tendencia central.
b. Medidas de Dispersión
Tal y como se adelantaba antes, otro aspecto a tener en cuenta al describir datos continuos es la dispersión de los mismos. Existen distintas formas de cuantificar esa variabilidad. De todas ellas, la varianza (S2) de los datos es la más utilizada. Es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Esta varianza muestral se obtiene como la suma de las de las diferencias de cuadrados y por tanto tiene como unidades de medida el cuadrado de las unidades de medida en que se mide la variable estudiada.
La desviación típica (S) es la raíz cuadrada de la varianza. Expresa la dispersión de la distribución y se expresa en las mismas unidades de medida de la variable. La desviación típica es la medida de dispersión más utilizada en estadística.
Aunque esta fórmula de la desviación típica muestral es correcta, en la práctica, la estadística nos interesa para realizar inferencias poblacionales, por lo que en el denominador se utiliza, en lugar de n, el valor n-1.
Por tanto, la medida que se utiliza es la cuasidesviación típica, dada por:
Aunque en muchos contextos se utiliza el término de desviación típica para referirse a ambas expresiones.
En los cálculos del ejercicio previo, la desviación típica muestral, que tiene como denominador n, el valor sería 20.678. A efectos de cálculo lo haremos como n-1 y el resultado seria 21,79.
El haber cambiado el denominador de n por n-1 está en relación al hecho de que esta segunda fórmula es una estimación más precisa de la desviación estándar verdadera de la población y posee las propiedades que necesitamos para realizar inferencias a la población.
Cuando se quieren señalar valores extremos en una distribución de datos, se suele utilizar la amplitud como medida de dispersión. La amplitud es la diferencia entre el valor mayor y el menor de la distribución.
Por ejemplo, utilizando los datos del ejemplo previo tendremos 80-15 =65.
Como medidas de variabilidad más importantes, conviene destacar algunas características de la varianza y desviación típica:
Otra medida que se suele utilizar es el coeficiente de variación (CV). Es una medida de dispersión relativa de los datos y se calcula dividiendo la desviación típica muestral por la media y multiplicando el cociente por 100. Su utilidad estriba en que nos permite comparar la dispersión o variabilidad de dos o más grupos. Así, por ejemplo, si tenemos el peso de 5 pacientes (70, 60, 56, 83 y 79 Kg) cuya media es de 69,6 kg. y su desviación típica (s) = 10,44 y la TAS de los mismos (150, 170, 135, 180 y 195 mmHg) cuya media es de 166 mmHg y su desviación típica de 21,3. La pregunta sería: ¿qué distribución es más dispersa, el peso o la tensión arterial? Si comparamos las desviaciones típicas observamos que la desviación típica de la tensión arterial es mucho mayor; sin embargo, no podemos comparar dos variables que tienen escalas de medidas diferentes, por lo que calculamos los coeficientes de variación
A la vista de los resultados, observamos que la variable peso tiene mayor dispersión.
Cuando los datos se distribuyen de forma simétrica (y ya hemos dicho que esto ocurre cuando los valores de su media y mediana están próximos), se usan para describir esa variable su media y desviación típica. En el caso de distribuciones asimétricas, la mediana y la amplitud son medidas más adecuadas. En este caso, se suelen utilizar además los cuartiles y percentiles.
Los cuartiles y percentiles no son medidas de tendencia central sino medidas de posición. El percentil es el valor de la variable que indica el porcentaje de una distribución que es igual o menor a esa cifra.
Así, por ejemplo, el percentil 80 es el valor de la variable que es igual o deja por debajo de sí al 80% del total de las puntuaciones. Los cuartiles son los valores de la variable que dejan por debajo de sí el 25%, 50% y el 75% del total de las puntuaciones y así tenemos por tanto el primer cuartil (Q1), el segundo (Q2) y el tercer cuartil (Q3).
Esta varianza muestral se obtiene como la suma de las de las diferencias de cuadrados y por tanto tiene como unidades de medida el cuadrado de las unidades de medida en que se mide la variable estudiada.
La desviación típica (S) es la raíz cuadrada de la varianza. Expresa la dispersión de la distribución y se expresa en las mismas unidades de medida de la variable. La desviación típica es la medida de dispersión más utilizada en estadística.
Aunque esta fórmula de la desviación típica muestral es correcta, en la práctica, la estadística nos interesa para realizar inferencias poblacionales, por lo que en el denominador se utiliza, en lugar de n, el valor n-1.
Por tanto, la medida que se utiliza es la cuasidesviación típica, dada por:
Aunque en muchos contextos se utiliza el término de desviación típica para referirse a ambas expresiones.
En los cálculos del ejercicio previo, la desviación típica muestral, que tiene como denominador n, el valor sería 20.678. A efectos de cálculo lo haremos como n-1 y el resultado seria 21,79.
El haber cambiado el denominador de n por n-1 está en relación al hecho de que esta segunda fórmula es una estimación más precisa de la desviación estándar verdadera de la población y posee las propiedades que necesitamos para realizar inferencias a la población.
Cuando se quieren señalar valores extremos en una distribución de datos, se suele utilizar la amplitud como medida de dispersión. La amplitud es la diferencia entre el valor mayor y el menor de la distribución.
Por ejemplo, utilizando los datos del ejemplo previo tendremos 80-15 =65.
Como medidas de variabilidad más importantes, conviene destacar algunas características de la varianza y desviación típica:
- Son índices que describen la variabilidad o dispersión y por tanto cuando los datos están muy alejados de la media, el numerador de sus fórmulas será grande y la varianza y la desviación típica lo serán.
- Al aumentar el tamaño de la muestra, disminuye la varianza y la desviación típica. Para reducir a la mitad la desviación típica, la muestra se tiene que multiplicar por 4.
- Cuando todos los datos de la distribución son iguales, la varianza y la desviación típica son iguales a 0.
- Para su cálculo se utilizan todos los datos de la distribución; por tanto, cualquier cambio de valor será detectado.
Otra medida que se suele utilizar es el coeficiente de variación (CV). Es una medida de dispersión relativa de los datos y se calcula dividiendo la desviación típica muestral por la media y multiplicando el cociente por 100. Su utilidad estriba en que nos permite comparar la dispersión o variabilidad de dos o más grupos. Así, por ejemplo, si tenemos el peso de 5 pacientes (70, 60, 56, 83 y 79 Kg) cuya media es de 69,6 kg. y su desviación típica (s) = 10,44 y la TAS de los mismos (150, 170, 135, 180 y 195 mmHg) cuya media es de 166 mmHg y su desviación típica de 21,3. La pregunta sería: ¿qué distribución es más dispersa, el peso o la tensión arterial? Si comparamos las desviaciones típicas observamos que la desviación típica de la tensión arterial es mucho mayor; sin embargo, no podemos comparar dos variables que tienen escalas de medidas diferentes, por lo que calculamos los coeficientes de variación
A la vista de los resultados, observamos que la variable peso tiene mayor dispersión.
Cuando los datos se distribuyen de forma simétrica (y ya hemos dicho que esto ocurre cuando los valores de su media y mediana están próximos), se usan para describir esa variable su media y desviación típica. En el caso de distribuciones asimétricas, la mediana y la amplitud son medidas más adecuadas. En este caso, se suelen utilizar además los cuartiles y percentiles.
Los cuartiles y percentiles no son medidas de tendencia central sino medidas de posición. El percentil es el valor de la variable que indica el porcentaje de una distribución que es igual o menor a esa cifra.
Así, por ejemplo, el percentil 80 es el valor de la variable que es igual o deja por debajo de sí al 80% del total de las puntuaciones. Los cuartiles son los valores de la variable que dejan por debajo de sí el 25%, 50% y el 75% del total de las puntuaciones y así tenemos por tanto el primer cuartil (Q1), el segundo (Q2) y el tercer cuartil (Q3).
a. Medidas de Tendencia Central
Las medidas de centralización vienen a responder a la primera pregunta. La medida más evidente que podemos calcular para describir un conjunto de observaciones numéricas es su valor medio. La media no es más que la suma de todos los valores de una variable dividida entre el número total de datos de los que se dispone.
Como ejemplo, consideremos 10 pacientes de edades 21 años, 32, 15, 59, 60, 61, 64, 60, 71, y 80. La media de edad de estos sujetos será de:
Más formalmente, si denotamos por (X1, X2,...,Xn) los n datos que tenemos recogidos de la variable en cuestión, el valor medio vendrá dado por:
Otra medida de tendencia central que se utiliza habitualmente es la mediana. Es la observación equidistante de los extremos.
La mediana del ejemplo anterior sería el valor que deja a la mitad de los datos por encima de dicho valor y a la otra mitad por debajo. Si ordenamos los datos de mayor a menor observamos la secuencia:
15, 21, 32, 59, 60, 60,61, 64, 71, 80.
Como quiera que en este ejemplo el número de observaciones es par (10 individuos), los dos valores que se encuentran en el medio son 60 y 60. Si realizamos el cálculo de la media de estos dos valores nos dará a su vez 60, que es el valor de la mediana.
Si la media y la mediana son iguales, la distribución de la variable es simétrica. La media es muy sensible a la variación de las puntuaciones. Sin embargo, la mediana es menos sensible a dichos cambios.
Por último, otra medida de tendencia central, no tan usual como las anteriores, es la moda, siendo éste el valor de la variable que presenta una mayor frecuencia.
En el ejemplo anterior el valor que más se repite es 60, que es la moda
Como ejemplo, consideremos 10 pacientes de edades 21 años, 32, 15, 59, 60, 61, 64, 60, 71, y 80. La media de edad de estos sujetos será de:
Más formalmente, si denotamos por (X1, X2,...,Xn) los n datos que tenemos recogidos de la variable en cuestión, el valor medio vendrá dado por:
Otra medida de tendencia central que se utiliza habitualmente es la mediana. Es la observación equidistante de los extremos.
La mediana del ejemplo anterior sería el valor que deja a la mitad de los datos por encima de dicho valor y a la otra mitad por debajo. Si ordenamos los datos de mayor a menor observamos la secuencia:
15, 21, 32, 59, 60, 60,61, 64, 71, 80.
Como quiera que en este ejemplo el número de observaciones es par (10 individuos), los dos valores que se encuentran en el medio son 60 y 60. Si realizamos el cálculo de la media de estos dos valores nos dará a su vez 60, que es el valor de la mediana.
Si la media y la mediana son iguales, la distribución de la variable es simétrica. La media es muy sensible a la variación de las puntuaciones. Sin embargo, la mediana es menos sensible a dichos cambios.
Por último, otra medida de tendencia central, no tan usual como las anteriores, es la moda, siendo éste el valor de la variable que presenta una mayor frecuencia.
En el ejemplo anterior el valor que más se repite es 60, que es la moda
Estadística Descriptiva
Una vez que se han recogido los valores que toman las variables de nuestro estudio (datos), procederemos al análisis descriptivo de los mismos. Para variables categóricas, como el sexo o el estadiaje, se quiere conocer el número de casos en cada una de las categorías, reflejando habitualmente el porcentaje que representan del total, y expresándolo en una tabla de frecuencias.
Para variables numéricas, en las que puede haber un gran número de valores observados distintos, se ha de optar por un método de análisis distinto, respondiendo a las siguientes preguntas:
a. ¿Alrededor de qué valor se agrupan los datos?
b. Supuesto que se agrupan alrededor de un número, ¿cómo lo hacen? ¿muy concentrados? ¿muy dispersos?
Suscribirse a:
Entradas (Atom)
